El problema de las n-reinas (I)

Definición

El puzle de las 8 reinas consiste en determinar la manera en la que se pueden colocar 8 reinas en un tablero de ajedrez sin atacarse entre ellas. El movimiento de la reina puede ser en cualquiera de las direcciones (vertical, horizontal, diagonales) y tantas casillas como se desee. Por ejemplo, una de las soluciones sería:

Solución válida al puzle de las 8 reinas.

El problema de las n-reinas es una variación del anterior en el que N reinas deben ser colocadas en un tablero de ajedrez de NxN casillas sin que se ataquen entre ellas. Existen soluciones para todos los números naturales excepto n=2, n=3.

Contando soluciones

Para encontrar o contar el número de soluciones al problema de las n-reinas, primero hay que distinguir entre un tablero solución y un tablero ilegal. Como se ha mencionado anteriormente, un tablero es solución del problema siempre y cuando que ninguna de las reinas se ataquen entre ellas. En otras palabras, por las características de su movimiento, dos reinas no pueden compartir columna/fila ni diagonal.

La manera más sencilla de representar un tablero es mediante un array unidimensional (o lista). Cada posición representa una fila del tablero y el valor la columna en la que se encuentra la reina. Por ejemplo:

board = [3, 1, 4, 2]

# - - Q -
# Q - - -
# - - - Q
# - Q - -

Equivalente a:

[3, 1, 4, 2]

Para determinar la legalidad de un tablero, basta con comprobar las condiciones mencionadas anteriormente:

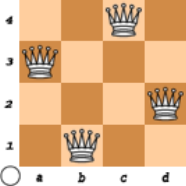
• No hay reinas que compartan la misma columna:

• No hay reinas que compartan la misma diagonal:

Sin embargo, al ser usado con permutaciones de una lista de números no repetidos (una reina por fila), nos podemos ahorrar la primera condición.

def check_legal(board):
    legal = True
    for i, ci in enumerate(board):
        for cj in board[(i + 1):]:
            if abs(ci - cj) == abs(board.index(ci) - board.index(cj)):
                legal = False
    return legal

Para contar el número de soluciones posibles para cada tamaño de n, hay que generar mediante permutaciones todas las configuraciones de tableros posibles:

def generate_configs(size):
    n_board = list(range(1, size + 1))
    # size = 5 -> n_board = [1, 2, 3, 4, 5]
    configs = itertools.permutations(n_board)
    return configs

Estas permutaciones sirven para «alimentar» la función siguiente, que comprueba la legalidad de todos estos tableros:

def check_if_legal(boards):
    count = 0
    for board in boards:
        n = len(board)
        if check_legal(board):
            count += 1
    print(f'{n} QUEENS | {count} legal boards')

Por último, para averiguar cuántas soluciones distintas (que no fundamentales) existen al problema de las n-reinas basta con usar la siguiente función, siendo n el número máximo de reinas a comprobar:

def check_n_queens(n):
    for i in range(1, n + 1):
        check_if_legal(generate_configs(i))

Por ejemplo, para contar el número de soluciones para n=1, 2, 3, … 10:

>>> check_n_queens(10)

1 QUEENS | 1 legal boards in 0.0 seconds
2 QUEENS | 0 legal boards in 0.0 seconds
3 QUEENS | 0 legal boards in 0.0 seconds
4 QUEENS | 2 legal boards in 0.0 seconds
5 QUEENS | 10 legal boards in 0.0010023117065429688 seconds
6 QUEENS | 4 legal boards in 0.00701904296875 seconds
7 QUEENS | 40 legal boards in 0.08622884750366211 seconds
8 QUEENS | 92 legal boards in 0.7836263179779053 seconds
9 QUEENS | 352 legal boards in 9.498818635940552 seconds
10 QUEENS | 724 legal boards in 114.95398807525635 seconds

Lo cual se corresponde con las enumeraciones oficiales de soluciones totales.